ペンシルパズルを自作して、唯一解判定ソルバーをSugar CSPソルバで作る
作成日: 2023-01-10
ペンシルパズルのルールを思いついたので、ペンシルパズルを自作しました。自作したペンシルパズルの唯一解性を保証するために、ソルバーを実装した話です。
このペンシルパズルのルール
(インストラクションレスとして例題を見るだけでも解けます。)
- すべてのマスに道を引く。
- 道は枝分かれや交差をしない。
- 手がかりの位置は道の始点のマスをすべて表す。
- すべての道は始点から右折だけを行って伸びる。
- 手がかりの数字はその道の右折の回数を表す。
ペンシルパズル問題は唯ー解でなくてはならない
ペンシルパズルの答えは、必ず1通りでなくてはなりません。さもなくば、誰かの答えと自分の答えが異なるという、悲惨な結果が待ち受けています。
今回のルールでは、答えから手がかりを生成することは簡単です。しかし、唯一解を保証するのはそこそこ大変です。実際、自分が最初に作った次のパズルは唯一解ではありませんでした。1手ずつ着実に解けるパズルでないと、唯一解性の保証は難しいのです。
唯一解でない問題を解きたいのならば、こちらから。正誤判定されません。
制約ソルバーSugarにペンシルパズルを解かせる
そこで、ペンシルパズルの手がかりから自動で答えを求めるプログラムを書いてみましょう。ペンシルパズルの実装といえば制約ソルバーです。今回は、ペンシルパズルを解くために作られたSugarという制約ソルバーを使ってみましょう。
Sugarは与えられた制約を満たす解を見つける
例えば、次のような制約を考えてみます。
(int x 0 1)
(int y 0 1)
(= (+ x y) 1)- 1、2行目は変数定義です。変数を定義しています。
- 3行目は制約定義です。です。
これをSugarに投げると、が得られます。
仮に、制約を満たす解が複数ある場合、その中の1つを発見した時点で解を返します。逆に、制約を満たす変数がありえない場合は、満たせないことを教えてくれます。
ペンシルパズルをSugarの制約に変換する
あとは、パズルからSugarの制約を生成すれば、パズルが解けます。制約を作ってみましょう。次のパズルを例にとって説明します。
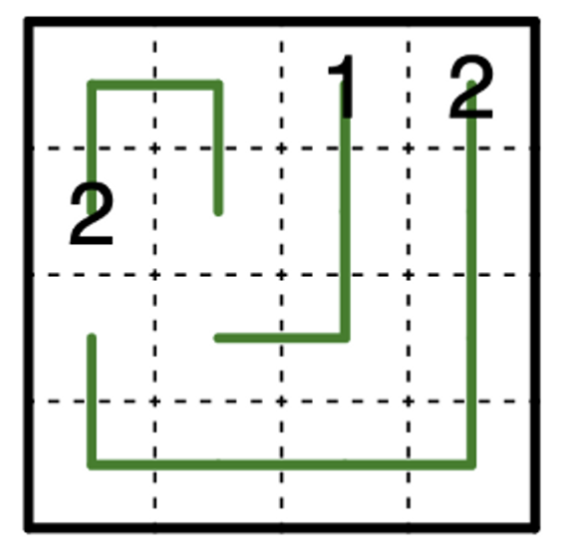
各マスがそれぞれ持つ変数情報
- Area: 通る道の手がかり番号 (1〜手がかりの数) ※手がかりごとに独立の番号をふる。
- Type: 直線か右折か始点か終点か (0直線、1右折、2始点、3終点)
- PathY: 下へ道があるか (-1逆向き、0なし、1順向き) ※道は向きがあるとする。
- PathX: 右へ道があるか(-1逆向き、0なし、1順向き)
- Order: 始点を1として道に連番を降ったときの数字 (1-全マス数)
以下は、一部分のマスについて変数を図解したものです。
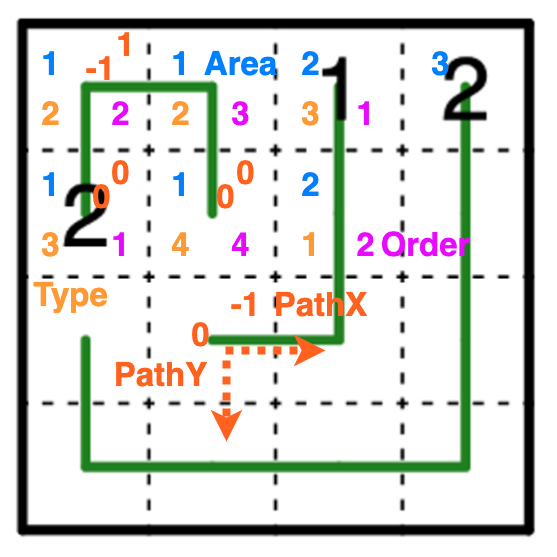
これらの変数にパズルのルールに即した制約をつけて行きます。
(制約StartPath) Type=始点は1本だけ道が始まる
- Type=始点か終点ならば、次のうち1が1つだけ、ほかの3つは0。
- 「このマスのPathX」
- -1 ×「左のマスのPathX」
- 「このマスのPathY」
- -1 ×「上のマスのPathY」
(制約EndPath) Type=終点は1本だけ道が終わる
制約StartPathと同様に-1が1つだけ。
(制約Straight) Type=直進ならば道は直進
- Type=直進のマスは次のどちらかを満たす;
- 「このマスのPathX」×「左のマスのPathX」= 1
- 「このマスのPathY」×「上のマスのPathY」= 1
(制約TurnRIght) Type=右折ならば道は右折
- Type=右折のマスはPathXとPathYがいい感じに右折
(制約StartHint) 始点は手がかりのあるところのみ
- マスに手がかりがあるならば、Area=手がかり番号、Type=始点
- なければ、Type≠始点
手がかり番号は、手がかり数字とは異なる、手がかりに独立に振った数です。
(制約Area) 道があるならば同じAreaに属する
- PathX≠0ならば、「このマスのArea」=「右のマスのArea」
- PathY≠0ならば、「このマスのArea」=「下のマスのArea」
(制約End) Areaごとに終点は1つ
- すべての手がかり番号Nについて、「Area=NかつType=終点となる変数」の個数=1
(制約NumberHint) Areaごとに手がかりの数だけ右折
- すべての手がかり番号Nについて、「Area=NかつType=右折となる変数」の個数=手がかり番号Nの数字
これらの制約で十分でしょうか?
Pathが道をしめし、道が手がかりの通り右折していることを表す制約は十分ありそうです。
しかし、実は制約が足りていません。道はループしないという制約が落ちています。次の図だと、始点と終点は1つずつあり、右折は4回しています。制約を満たしています。
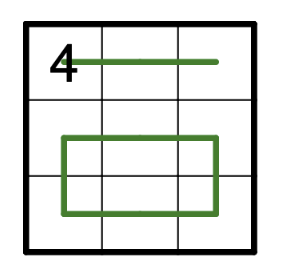
この場合は道が一続きではないので、ルールに適合していません。このようなループを除外するために、道に順番に数字を振ります。ループには順番に数字を振ることが出来ないので、ループが解になることがなくなります。
(制約NoLoop) 道に沿って1から順番に数字を振ることができる
- Type=始点
- PathX=1ならば、「このマスのOrder」+ 1 =「右のマスのOrder」
- PathX=-1ならば、「このマスのOrder」- 1 =「右のマスのOrder」
- PathY=1ならば、「このマスのOrder」+ 1 =「下のマスのOrder」
- PathY=-1ならば、「このマスのOrder」- 1 =「下のマスのOrder」
出来た制約をSugarに投げる
最終的にはこんな制約になります。
Sugarに投げると制約を満たす変数例が得られました。いい感じですね。
s SATISFIABLE
; Size 4x4
;# Area variables
; 3 3 1 2
; 3 3 1 2
; 2 1 1 2
; 2 2 2 2
;# Type variables
; 1 1 2 2
; 2 3 0 0
; 3 3 1 0
; 1 0 0 1
;# Path variables
; +--+ + +
; ! | | |
; + + + +
; | |
; + +~~+ +
; ! |
; +~~+~~+~~+解を除外して唯一解判定をする
Sugarは解を1つ見つけた時点で終了します。唯一解判定をするには、見つけた解を除外する制約をパズルの制約に追加して、もう一度Sugarに投げます。
s UNSATISFIABLE見つけた解を除外すると、他に解がないようです。無事に、このパズルが唯一解であることがわかりました。